Integration by parts worksheet with answers

2ex cosx dx ex cosx ex sin x C ex x dx ex cosx ex sin x C 2 1 cos Answer Note. We use integration by parts a second time to evaluate.

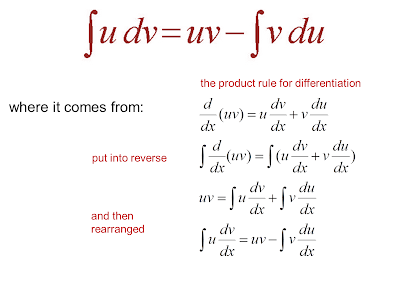
Let dv e x dx then v e x.

Integration by parts worksheet with answers. Note appearance of original integral on right side of equation. Move to left side and solve for integral as follows. 2ex cosx dx ex cosx ex sin x C ex x dx ex cosx ex sin x C 2 1 cos Answer Note.

After each application of integration by parts watch for the appearance of a constant multiple of the original integral. Calculus Integration by Parts Worksheets. These Calculus Worksheets will produce problems that involve solving indefinite integrals by using integration by parts.

The student will be given functions and will be asked to find their indefinite integral. You may select the number of problems per worksheet and whether to give the values of u and dv to substitute in. The following are solutions to the Integration by Parts practice problems posted November 9.

Let u sinx dv exdx. Then du cosxdxand v ex. Then Z exsinxdx exsinx Z excosxdx Now we need to use integration by parts on the second integral.

Let u cosx dv exdx. Then du sinxdxand v ex. Then Z exsinxdx exsinx excosx Z.

Q H LA 3l 9l V QrXiBgkh zt3sV er 2eos Qesr1v pesd gB Y ZMNaLd YeM Kw ni yt nhE oI9n Qffi zn hiwtLeK lC Kaml2c9uvlduAsV3 Worksheet by Kuta Software LLC Kuta Software - Infinite Calculus Name_____ Integration by Parts Date_____ Period____ Evaluate each indefinite integral using integration by parts. INTEGRATION BY PARTS WORKSHEET 1 Integrate the following with respect to x. Converting customary units worksheet.

Converting metric units worksheet. Integration by Parts Worksheet. I believe in free education - all my resources are free.

Here is a set of practice problems to accompany the Integration by Parts section of the Applications of Integrals chapter of the notes for Paul Dawkins Calculus II course at Lamar University. Integration by parts mc-stack-TY-parts-2009-1 A special rule integrationbyparts is available for integrating products of two functions. This unit derives and.

Now integrating both sides with respect to x results in Z u dv dx dx uv Z du dx vdx This gives us a rule for integration called INTEGRATION BY PARTS that allows us to integrate many products of functions of x. We take one factor in this product to be u this also appears on the right-hand-side along with du dx. The other factor is.

This booklet contains the worksheets for Math 1B UC. Berkeleys second semester. Use integration by parts to prove the reduction formula Z lnxn dx xlnxn n Z.

Remember that your answer needs to be expressed in terms of the original variable in this case x or t. Integration by parts mc-TY-parts-2009-1 A special rule integrationbyparts is available for integrating products of two functions. So we have done integration by parts twice to arrive at our final answer.

Remember that to apply the formula you have to be able to integrate the function you call dv dx. Integration by parts is used to integrate a product. At this point we have part of the final answer but we still have an integral.

Reevaluate this integral and integrate it by any appropriate method. From the 1998 BC Multiple Choice. Showing top 8 worksheets in the category - Integration By Parts.

Some of the worksheets displayed are 05 25integration by parts Work 4 integration by parts Integration by parts Math 114 work 1 integration by parts Math 34b integration work solutions Math 1020 work basic integration and evaluate Work introduction to integration. Using the Integration by Parts formula. We use integration by parts a second time to evaluate.

Let u x the du dx. Let dv e x dx then v e x. Substituting into equation 1 we get.

Integration by parts - choosing u and dv How to use the LIATE mnemonic for choosing u and dv in integration by parts. U-substitution and integration by parts Name. U-substitutionchange of variables - undoing the chain rule.

Given R b a fgxg0x dx substitute u. Worksheet 54Integration by Parts Show all work. No calculator unless stated.

If ³³xxdxhx xxdxcos 2 sin 2 then hx A 2sin 2 cosxx xC B xxC2 sin C 2cos sinxxx xC 2 D 4cos 2 sinxx xC E 2cos4sin xx xC2 2. ³xxdxsin 5 A xx xCcos 5 sin 5 B 1 cos 5 sin 5 525 x. 1View Solution 2View Solution 3View Solution 4View SolutionPart a.

Z 7 p 1 2u du. The integral equals 7arcsinu. Z r2 2r 1 r dr.

The integral evaluates as 1 3 r3 2 ln jr C. Z 4sinx 3tanx dx The integrand simpli es to 4 3 cosx. Therefore the integral is 4 3 sinx C.

Thats 7sinx 4ex C. Z 3 p 7vdv. Since you can rewrite the.

Basic Integration Problems I. Find the following integrals. 5 8 5x x dx2 2.

6 9 4 3x x x dx32 3 3. 2 3x x dx 2 23 8 5 6 4. Dx x xx 1 5.

3 x dx.